Eric William Hester

Eric William Hester

Lecturer

University of Bath

Interests

Applied Mathematics
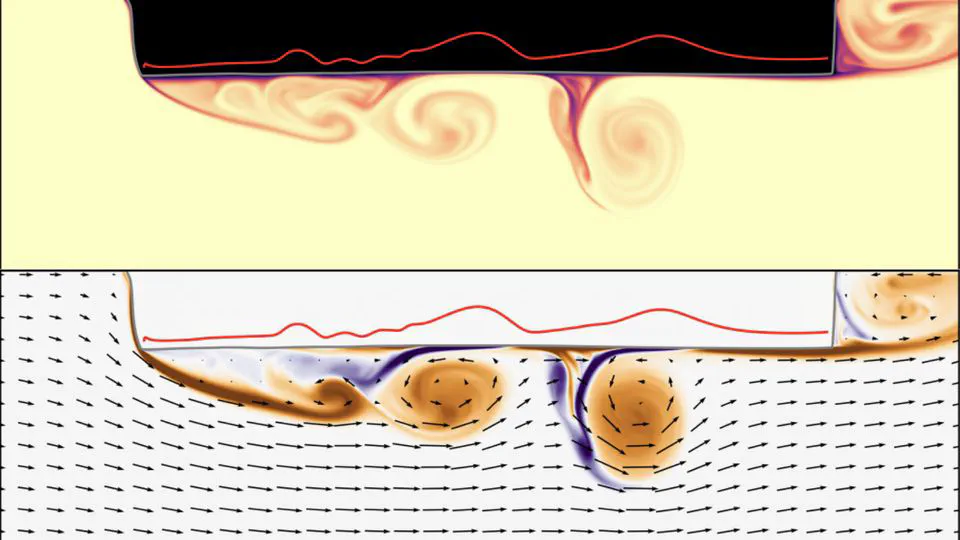
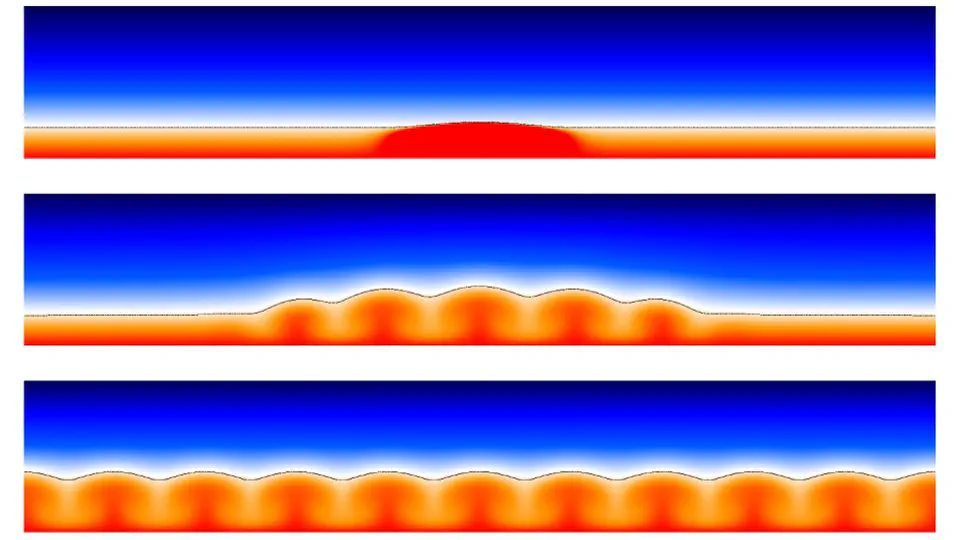
Fluid Dynamics
Asymptotics
Numerical Analysis
The Dedalus PDE solver

Education

Doctor of Philosophy in Applied Mathematics
The University of Sydney
Bachelor of Science (Advanced) (Honours)
The University of Sydney

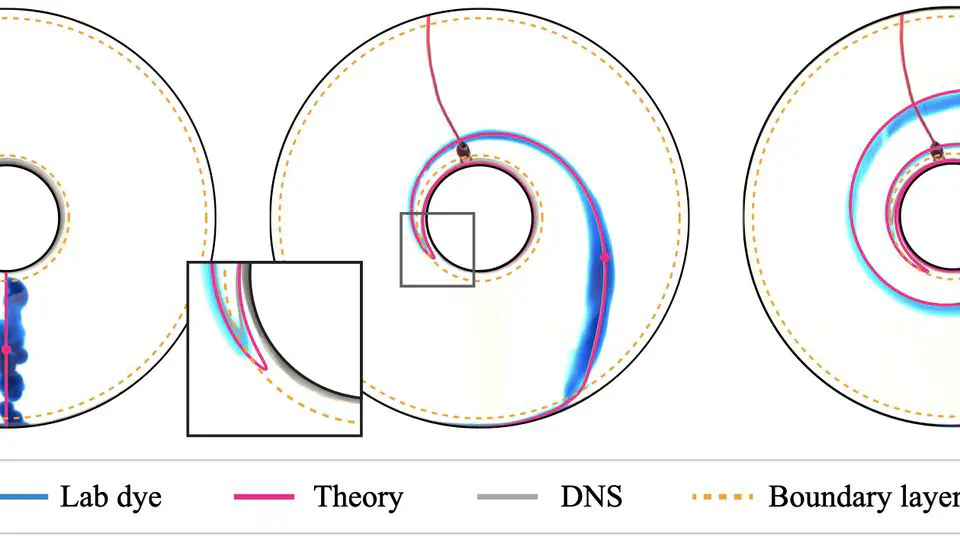
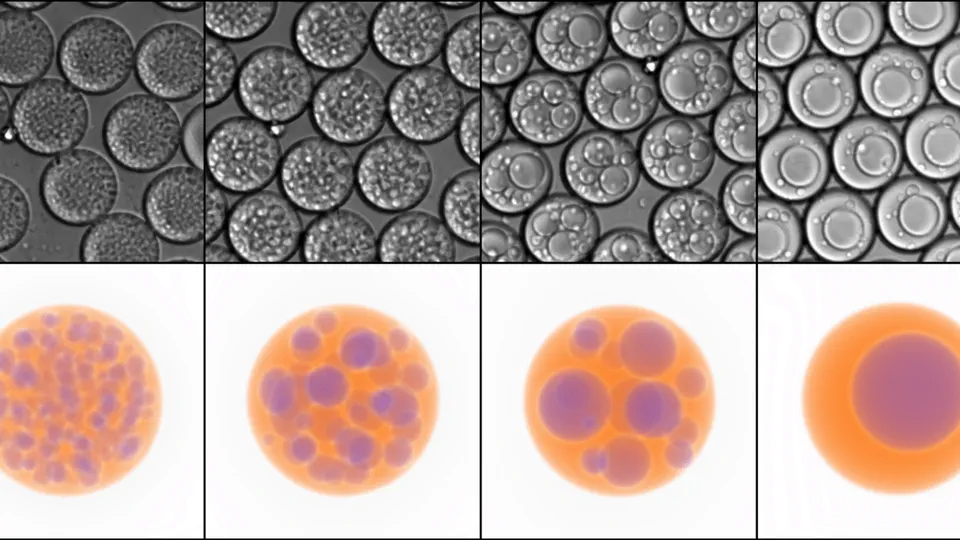
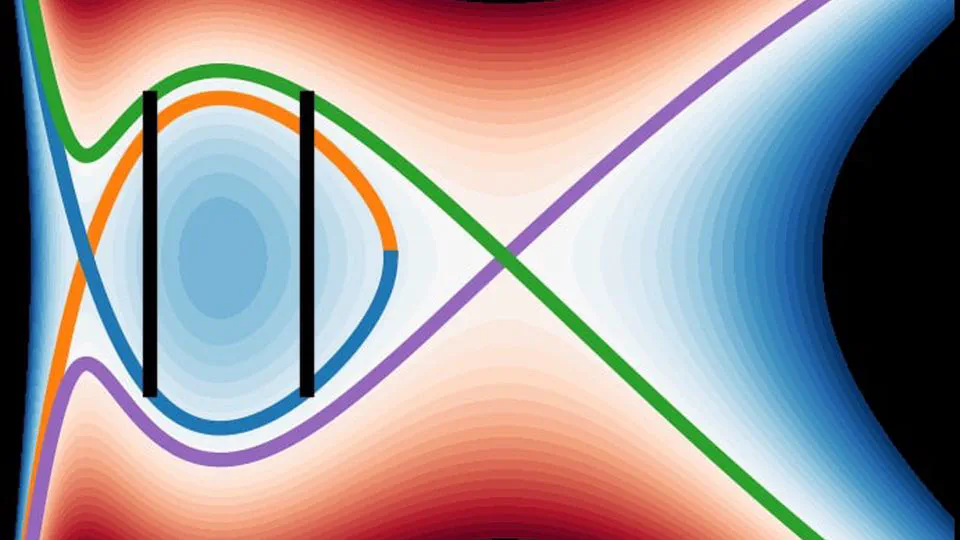
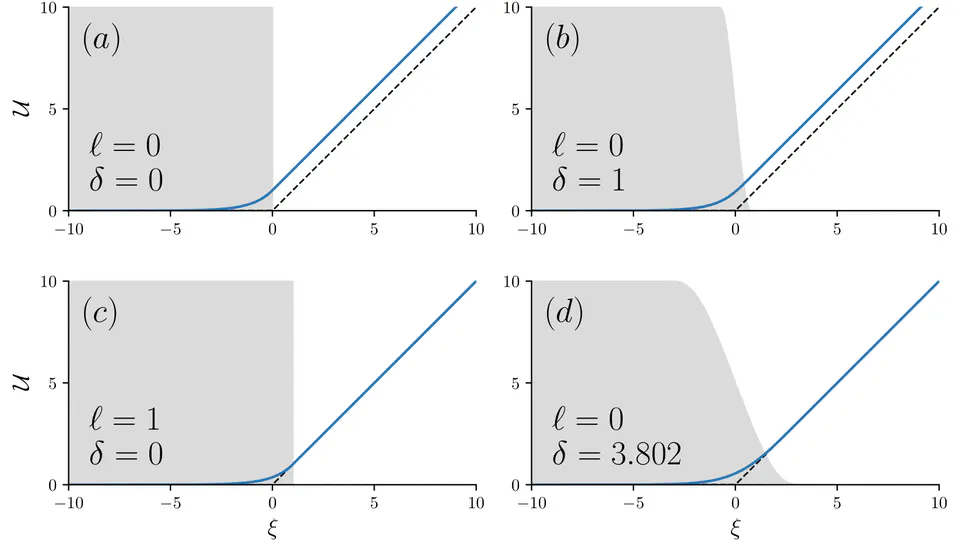
My Research

I am a Lecturer in Applied Mathematics at the University of Bath. I’m interested in all aspects of fluid dynamics, numerical PDEs, and asymptotic methods.

Publications

Magneto-Stokes Flow in a Shallow Free-Surface Annulus

Magnetohydrodynamics

Magneto-Stokes Flow in a Shallow Free-Surface Annulus

We analyse magneto-Stokes flow in the cylindrical-annular geometry of the Taylor-Couette cell, developing a compplete analytical solution that we verify in laboratory experiments and direct numerical simulations in Dedalus. We also investigate optimal parameters for enhanced mixing devices.

Oct 1, 2024

Fluid dynamics alters liquid–liquid phase separation in confined aqueous two-phase systems

Fluid dynamics alters liquid–liquid phase separation in confined aqueous two-phase systems

We model temperature-induced phase separation in aqueous polymers used to manufacture Janus droplet microparticles at UCLA startup Partillion Bioscience. Fluid flow and buoyancy greatly alters separation speed, as well as equilibrium droplet shapes. We propose channel flow as a cheap method to accelerate separation tenfold.

Dec 5, 2023

Double-Diffusive Layer and Meltwater Plume Effects on Ice Face Scalloping in Phase-Change Simulations

Ice-Ocean Interactions

Double-Diffusive Layer and Meltwater Plume Effects on Ice Face Scalloping in Phase-Change Simulations

We simulate turbulent double-diffusive plumes near a vertical ice face and observe spontaneous generation of scalloped topography.

Sep 18, 2023

Orthogonal signed-distance coordinates and vector calculus near evolving curves and surfaces

Differential Geometry

Orthogonal signed-distance coordinates and vector calculus near evolving curves and surfaces

An elementary derivation of a convenient and elegant coordinate systems for neighbourhoods of curves and surfaces.

May 11, 2023

On the stability of shocks in isothermal black hole accretion discs

Astrophysical Fluid Dynamics

On the stability of shocks in isothermal black hole accretion discs

We add infinitesimal dissipation to show uniqueness of isothermal shocks in black hole accretion disks. But these shocks are only stable in a much narrower range parameter space than previously believed.

Jun 12, 2022

Aspect Ratio Affects Iceberg Melting

Ice-Ocean Interactions

Aspect Ratio Affects Iceberg Melting

We analyse the influence of geometry on iceberg melting in a combination of laboratory experiment and direct numerical simulation, proposing a new geometry-aware parameterisation of iceberg melting.

Aug 29, 2021

Topography generation by melting and freezing in a turbulent shear flow

Ice-Ocean Interactions

Topography generation by melting and freezing in a turbulent shear flow

We simulate turbulent three-dimensional flow beneath an ice layer and observe spontaneous stratification-dependent generation of topography.

Mar 12, 2021

Improving convergence of volume penalised fluid-solid interactions

Volume Penalty Method

Improving convergence of volume penalised fluid-solid interactions

We derive higher-order accurate volume-penalty models with no added implementation cost, and verify their accuracy in several benchmark problems in Dedalus.

Oct 21, 2020

Improved phase-field models of melting and dissolution in multi-component flows

Phase Field Models

Improved phase-field models of melting and dissolution in multi-component flows

We develop the first second-order phase-field model to combine melting and dissolution in multi-component flows, and validate our asymptotics against a suite of numerical benchmarks.

Jun 30, 2020

Bistability in Rayleigh-Bénard convection with a melting boundary

Ice-Ocean Interactions

Bistability in Rayleigh-Bénard convection with a melting boundary

We demonstrate bistability in Rayleigh-Benard convection by considering a melting upper boundary.

Feb 5, 2020