Bistability in Rayleigh-Bénard convection with a melting boundary
Feb 5, 2020·,,,·
0 min read
Jhaswantsing Purseed
Benjamin Favier
Laurent Duchemin
Eric W. Hester
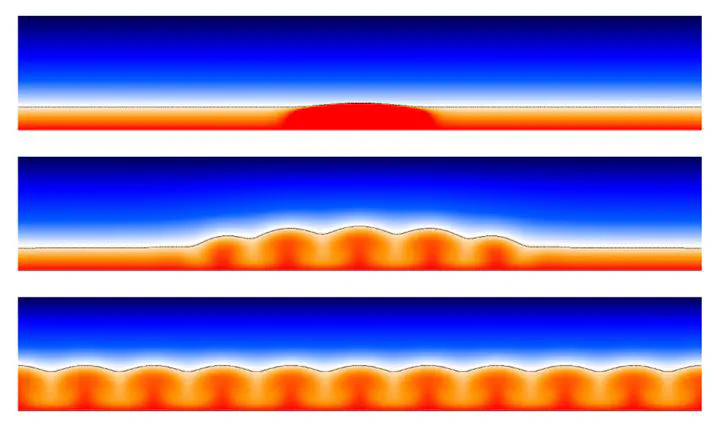 Bistability in melting patterns above convecting fluids.
Bistability in melting patterns above convecting fluids.Abstract
A pure and incompressible material is confined between two plates such that it is heated from below and cooled from above. When its melting temperature is comprised between these two imposed temperatures, an interface separating liquid and solid phases appears. Depending on the initial conditions, freezing or melting occurs until the interface eventually converges toward a stationary state. This evolution is studied numerically in a two-dimensional configuration using a phase-field method coupled with the Navier-Stokes equations. Varying the control parameters of the model, we exhibit two types of equilibria: diffusive and convective. In the latter case, Rayleigh-Bénard convection in the liquid phase shapes the solid-liquid front, and a macroscopic topography is observed. A simple way of predicting these equilibrium positions is discussed and then compared with the numerical simulations. In some parameter regimes, we show that multiple equilibria can coexist depending on the initial conditions. We also demonstrate that, in this bistable regime, transitioning from the diffusive to the convective equilibrium is inherently a nonlinear mechanism involving finite-amplitude perturbations.
Type
Publication
Physical Review Fluids